NFV/SDNネットワークにおけるサービスチェイニング

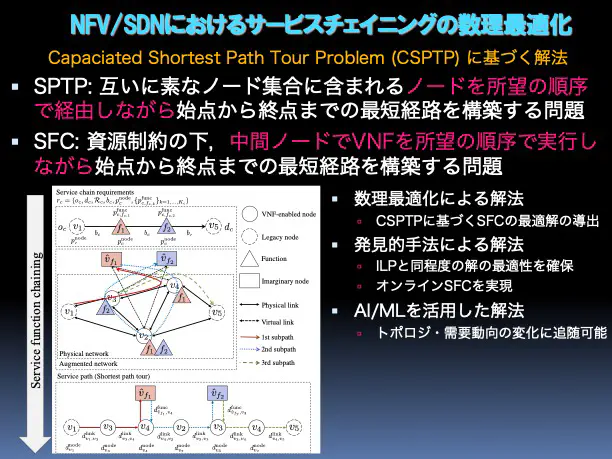
Network Fucntions Virtualization（NFV）はネットワーク機能を従来の専用機器から分離し，仮想ネットワーク機能（VNF）として汎用機器上で実行することで，拡張性と柔軟性を備えたネットワークサービスを提供できます． 一方で，Software Defined Networking (SDN) はデータプレーンからコントロールプレーンを分離し，集中制御機能によってプログラマブルネットワーキングを実現できます． 両者は互いに補完的であり，NFVにおける資源割当問題の一つであるサービスチェイニング (Service Function Chaining: SFC) を実現するための基盤技術の一つです． SFC問題は，資源制約の下，中間ノードでVNFを所望の順序で実行しながら始点から終点までの最短経路を構築する問題です． この問題は最短経路ツアー問題 (Shortest Path Tour Problem: SPTP) との類似性が指摘されており，本研究ではその類似性に着目し，SPTPの助けを借りて効率的にSFCを実現する手法を実現することを目的としています¹． さらに，ラグランジュ緩和を利用したオンラインSFCの実現も目指しています²．

Shortest Path Tour Problem (SPTP)

互いに素なノード集合$\mathcal{T}_1, \ldots, \mathcal{T}_k (\mathcal{T}_1 \cap \ldots \cap \mathcal{T}_k = \emptyset, k \geq 1)$に含まれるノードを所望の順序で経由しながら，始点から終点までの最短路を計算する問題．

定義

• 有向グラフ: $G = (\mathcal{V}, \mathcal{E})$．
• $\mathcal{V}$: 頂点集合，$\mathcal{E}$: 辺集合．
• $\mathcal{T}_K \subset \mathcal{V}$ $(\mathcal{T}_1 \cap \ldots \cap \mathcal{T}_K = \emptyset, K \geq 1)$: $k$番目に経由するノード集合
• $s, d \in \mathcal{V}$ $(s \neq d)$: 始点，終点

解法

• ILPの定式化
• グラフ変換し，Dijkstra法を適用する．
• Depth first tour search algorithm

定式化

SPTPを定式化するために，グラフ$G$を下記図ようなグラフ$G^+ = (\mathcal{V}^+, \mathcal{E}^+)$に拡張する．

ここで，$\mathcal{V}^+ = \mathcal{V} \cup \hat{\mathcal{V}}$, $\mathcal{E}^+ = \mathcal{E} \cup \hat{\mathcal{E}}$である． $\hat{\mathcal{V}}$は拡張ノードの集合である $(\hat{\mathcal{V}} = \cup_{k=1, \ldots, K} \{ \hat{v}_k \} )$ ． $\hat{\mathcal{E}}$はノード $i \in \mathcal{T}_k$ と拡張ノード$\hat{v}_k \in \hat{\mathcal{V}}$を結ぶリンク $(i, \hat{v}_k)$ の集合である．なお，当該リンクのコストは0とする．

グラフ$G^+$より，SPTPは下記式で定式化できる．

\begin{align} \newcommand\E{\mathcal{E}} \newcommand\V{\mathcal{V}} \min \quad & \sum_{k=1}^{K+1} \sum_{(i, j) \in \E}x_{i,j}^{k} d_{i,j}, \tag{1} \\ \mathrm{s.t.} \quad & x_{i,j}^{k} = \{0, 1\}, \quad (i, j) \in \E^+, \forall k = 1, \ldots, K+1, \tag{2} \\ & \sum_{(i, j) \in \E^+} x_{i,j}^{k} - \sum_{(j, i) \in \E^+} x_{j,i}^{k} = \begin{cases} 1 & \textrm{if $i = a_k$}\\ -1 & \textrm{if $i = b_k$},\\ 0 & \textrm{otherwise.} \end{cases} \\ & \quad \forall k = 1, \ldots, K+1, \forall i \in \V^+, \tag{3} \\ & x_{i,\hat{v_k}}^k \leq x_{\hat{v_k}, i}^{k+1}, \quad k = 1, \ldots, K, \forall (i, \hat{v_k}) \in \E^+, \tag{4} \\ & x_{i,\hat{v}_m}^k = 0, \quad \forall (i, \hat{v}_m) \in \E^+, k = 1, \ldots, K, m \neq k, \tag{5} \\ \end{align}

(1) は目的関数を表している． ここで，$d_{i,j}$はリンク$(i, j)$のコストを表している． (2) はバイナリ変数を表しており，$k$番目のサブパスにおいて，リンク$(i,j)$を利用する場合は1を取り，それ以外は0を取る． (3) は各$k$番目のサブパスにおけるフローの保存則を表している． (4) は$k$番目のサブパスと$k+1$番目のサブパスの接続性を保証している． (5) は$k$番目のサブパスにおいて，$\hat{v}_m$を経由することを禁止している．

Constrained SPTP

リンク利用を高々1回に制限したSPTP． この問題はNP困難であることが知られている．

定式化

\begin{align} \newcommand\E{\mathcal{E}} \newcommand\V{\mathcal{V}} \min \quad & (1), \\ \textrm{s.t.} \quad & (2)–(5), \\ & \sum_{k=0}^{K+1}x_{i,j}^k \leq 1, \quad \forall (i,j) \in \E \tag{6} \\ \end{align}

(6)は各リンクを高々1回利用できる制約である．

Capacitated SPTP for SFC

ノード・リンクの容量制約を実数で与えたSPTP¹．

定式化

\begin{align} \newcommand\E{\mathcal{E}} \newcommand\V{\mathcal{V}} \min \quad & (1), \\ \textrm{s.t.} \quad & (2)–(5), \\ & b\sum_{k=0}^{K+1}x_{i,j}^k \leq B_{i,j}, \quad \forall (i,j) \in \E \tag{7} \\ \end{align}

ここで，$b$はフロー量，$B_{i,j}$はリンク$(i, j)$の容量を表す． (7)はリンクの容量制約を表している．